Phân loại là việc gán một phần tử thích hợp nhất vào các tổng thể đã được biết trước dựa vào các biến quan sát. Nó là một hướng phát triển quan trọng của thống kê nhiều chiều, có vai trò nền tảng trong lĩnh vực khai phá dữ liệu. Bài toán phân loại đã và đang được áp dụng đa dạng trong các lĩnh vực nên hiện tại được rất nhiều nhà thống kê và công nghệ thông tin quan tâm. Về mặt lý thuyết, hiện có bốn phương pháp chính để giải quyết bài toán phân loại: phương pháp Fisher, hồi qui logistic, SVM (super vector machine) và Bayes. Phương pháp Fisher ra đời sớm nhất, có thể phân loại cho hai hay nhiều hơn hai tổng thể nhưng phải giả thiết ma trận hiệp phương sai của các tổng thể bằng nhau nên có nhiều hạn chế trong áp dụng thực tế. Hiện nay, phương pháp hồi qui logistic được sử dụng phổ biến, nhưng chỉ hiệu quả khi dữ liệu có sự tách rời tốt của các nhóm và biến phụ thuộc là nhị phân. Phương pháp SVM tận dụng sự phát triển của công nghệ thông tin, xây dựng mô hình dựa trên dữ liệu tập huấn luyện và tập kiểm tra nên đòi hỏi dữ liệu lớn. Phương pháp Bayes được xem có nhiều ưu điểm, có thể phân loại được cho hai hay nhiều hơn hai tổng thể. Phương pháp này cũng không bị ràng buộc bởi các giả thiết phân phối chuẩn và phương sai bằng nhau của các tổng thể. Các kết quả nghiên cứu mới trong những năm gần đây về bài toán phân loại chủ yếu tập trung xung quanh phương pháp Bayes.

Trong áp dụng thực tế hiện nay, phương pháp Bayes được sử dụng khá hạn chế. Trong hạn chế này, vấn đề xác định xác suất tiên nghiệm, ước lượng hàm mật độ xác suất và sự tính toán phức tạp của phương pháp này là những nguyên nhân chính. Xác suất tiên nghiệm thường được xác định dựa vào kinh nghiệm, sự hiểu biết của người thực hiện, hoặc một tổng kết thống kê trước đó cho vấn đề mà ta cần phân loại. Một số đề xuất dựa vào thống kê cũng được xem xét và áp dụng như phân phối đều, tỉ lệ mẫu, phương pháp Laplace. Tuy nhiên chúng chỉ phù hợp cho từng bộ dữ liệu mà không phải là tất cả. Bên cạnh xác suất tiên nghiệm, khi thực hiện bài toán phân loại bằng phương pháp Bayes, chúng ta phải ước lượng hàm mật độ xác suất. Mặc dù có nhiều cải tiến trong những năm gần đây, nhưng cho đến nay nó vẫn còn nhiều hạn chế. Ngoài hai vấn đề trên, những phức tạp trong tính toán như tìm hàm cực đại, tính tích phân trong không gian nhiều chiều cũng là cản trở chính trong áp dụng thực tế của phương pháp này. Dựa trên bài toán phân tích chùm mờ nghiên cứu đề xuất thuật toán xác định xác suất tiên nghiệm phù hợp cho từng bộ dữ liệu và cho từng phần tử cần phân loại. Nghiên cứu này cũng đề nghị phương pháp ước lượng hàm mật độ xác suất từ số liệu rời rạc và áp dụng phương pháp Monte Carlo để giải quyết vấn đề tính toán trong thực tế của phương pháp Bayes.

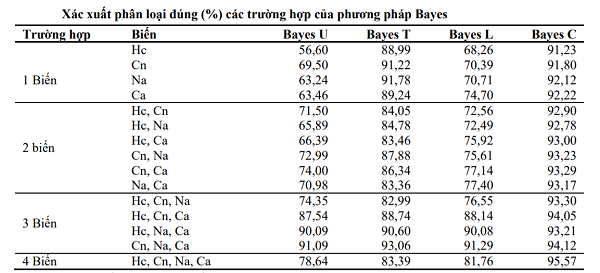
Hiện nay bài toán phân loại được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau. Trong y học, bài toán phân loại được ứng dụng theo hai hướng sau:

i) Có k loại bệnh đều được phát hiện dựa vào n biến quan sát định tính hoặc định lượng. Một người có các chỉ số sinh hóa cụ thể, dựa vào các phương pháp phân loại, chúng ta cần kết luận người đó bị bệnh nào trong số k loại bệnh đã biết.

ii) Chúng ta đang quan tâm một loại bệnh cụ thể B nào đó của một người. Dựa trên n biến quan sát định tính hoặc định lượng của người này, cần kết luận người này có khả năng bị bệnh B hay không.

Cả hai vấn đề này thực chất là việc giải quyết bài toán phân loại cho hai tổng thể và nhiều hơn hai tổng thể. Vì vậy nghiên cứu này sẽ áp dụng những cải tiến trong thực tế của phương pháp Bayes được đề cập ở trên vào lĩnh vực y học.

Phần tiếp theo của bài báo được cấu trúc như sau. Phần 2 trình bày phương pháp Bayes và thuật toán đề nghị trong phân loại bệnh. Phần 3 giải quyết các vấn đề áp dụng thực tế của thuật toán đề nghị. Phần 4 áp dụng thuật toán cho một số liệu thực tế. Phần cuối cùng là kết luận của bài viết.

Nghiên cứu phương pháp phân loại Bayes với những cải tiến và đề xuất để áp dụng được cho dữ liệu rời rạc của thực tế. Đó là vấn đề xác định xác suất tiên nghiệm, ước lượng hàm mật độ xác suất và tính sai số Bayes. Nghiên cứu đã xây dựng một chương trình trên phần mềm Matlab để thực hiện hiệu quả cho số liệu thực. Từ những cải tiến này, nghiên cứu đã đề xuất được thuật toán phân loại bệnh trong y học. Thuật toán này đã được áp dụng hiệu quả cho một tập dữ liệu thực. Thuật toán đề nghị cũng có thể áp dụng tương tự cho nhiều lĩnh vực khác. Nếu có số liệu đủ lớn và tin cậy, bài toán phân loại có thể trở thành một công cụ quan trọng hỗ trợ ngành y trong nghiên cứu chẩn đoán bệnh. Chúng tôi sẽ tiếp tục nghiên cứu đề xuất các phương pháp để chẩn đoán một số bệnh khác trong thời gian sắp tới dựa vào các số liệu thực tế ở Việt Nam.

lttsuong